Chapter 3
PERIKINETIC COAGULATION AT MICRO-G CONDITIONS
Abstract:
In this chapter, perikinetic coagulation experiments are reported which were
performed at 1g and µg conditions during a flight in a sounding rocket
(TEXUS 31), for dispersions of polystyrene, quartz and silica particles. Three
different experiments were performed with the polystyrene dispersion: one in
which the densities of the PS-particles and the continuous phase were matched,
one in which the density of the continuous phase was lower than the PS-particles
and one in which the density of the continuous phase was higher than the PS-particles.
With the silica and quartz dispersions, only experiments were performed in which
the density of the continuous phase was lower than the density of the particles.
Coagulation rates for dispersions of polystyrene, quartz and silica are found
to increase significantly at µg conditions compared to 1g conditions.
The most pronounced effect is found for the polystyrene dispersions with a small
density difference between the dispersed and the continuous phase.
3.1 Introduction
Krutzer
[1] studied the influence of flow type, particle type and gravity on orthokinetic
coagulation. Among others before Krutzer, Van Diemen and Stein [2], Logtenberg
[3] and Brakalov et al. [4], performed shear induced coagulation experiments
under 1g conditions. Their experiments showed a slower coagulation than theoretically
expected. Conclusions from these experiments were uncertain because of the interplay
of several factors; the changed attraction as a result of deviations of the
particle shape from a spherical shape, the complicated nature of the flow pattern
in the experimental set-up, the role of inertia and the interplay of Brownian,
shear-induced and gravity-induced coagulation.
Van de Ven and Mason [5] and Zeichner and Schowalter [6], performed theoretical
calculations which all refer to spherical particles in the absence of inertia.
Coagulation is impossible, when there is no interaction between two particles.
The trajectories of the particles can be divided into `open' and `closed' ones,
separated by a `limiting' trajectory. In the absence of interparticle forces
it is impossible for a particle to cross a limiting trajectory, thus either
two particles (initially at larger distance than corresponds with the limiting
trajectory) will never meet or two particles (initially at smaller distance
than corresponds with the limiting trajectory) will never be separated. However,
when attractive London- Van der Waals forces are operative it is possible for
an approaching particle to cross the limiting trajectory and coagulation can
occur.
Logtenberg [3], concluded from his trajectory calculations that for spherical
particles with a radius of 10-7 m to 10-6 m, inertia forces
do not play a role of importance.
In order to get a better understanding of the influence of inertia forces on
coagulation, Krutzer [1], performed coagulation experiments at different shear
rates at µg conditions (prevention of sedimentation). He found that at low shear
rates, coagulation proceeds faster at µg conditions than at 1g conditions.
In order to get a better understanding
of the inertia forces and the interplay of gravity and Brownian-induced coagulation
we performed perikinetic coagulation experiments at µg conditions (10-4g),
during a flight in a sounding rocket (TEXUS 31: `Technologische EXperimente
Unter Schwerelosigkeit'). In this experiment not only polystyrene but also quartz
and silica dispersions were used. Because of the high density of quartz and
silica, and the relatively large size of the particles, entailing rapid sedimentation,
these dispersions could not be used in the experiments reported in chapter 4
(1g and high-g).
The experiments described
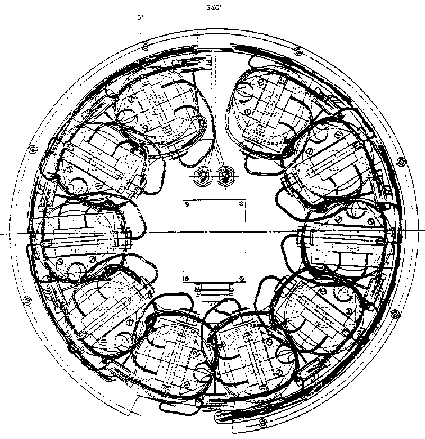
in the present chapter were carried out in the TEM 06-12 module, which is shown
in figure 3.1 (top view representation). The TEM 06-12 module contains ten measuring
utilities, in which five duplicate experiments were performed: three with a
polystyrene dispersion, D r
<0; D r
=0; D r >0,
one with silica D r
<0 and one with quartz D
r <0
(D r = r
medium - r
disperse phase).
As mentioned in chapter 2,
the light intensity measurements, for following coagulation, were performed
at a detection angle of f £
2° , because the light intensity at 0° was too high for the detection
equipment used at the launch base. As concluded in chapter 2, this has no consequences
for the interpretation of the results.
The TEXUS 31 rocket was launched from the Esrange launch base (november 1993)
near Kiruna in Sweden. After extensive testing, the module was implemented in
the rocket, together with four other modules of other experimenters. The launch
time of the rocket was determined by weather condition requirements. The testing
of the experimental module before flight, is discussed in section 3.2. The rocket
reached a height of approximately 270 kilometres, then the spin (rotation of
the rocket around its axis) was stopped and the µg period, which lasted about
six minutes, started.
At the end of the flight, a parachute ensured a gentle landing of the rocket
on the ground. A helicopter recovered the rocket, within 45 minutes.

Figure 3.1: Top view representation of the TEXUS TEM 06-12 module, consisting of 10 coagulation cells, light sources and detectors and the steering electronics.
Polystyrene-latex
The method for the preparation of
the polystyrene latex is described in [7]. The polystyrene latex (L-93) particles
used for these coagulation experiments had a number averaged diameter of 1.879
m m (see for the codes of the various polystyrene dispersions section 2.2).
Their volume averaged diameter was 2.030 m m. These particle sizes were
determined with the Coulter LS-130. In this apparatus and accompanying software,
the particle size is calculated on static light scattering using Fraunhofer
diffraction for large particles and Mie-scattering for intermediate sizes (1
< d < 10 m m, in combination with Polarization Intensity Differential
Scattering for small particles [8]). The density of the polystyrene, as measured
by means of a Paar DMA-10 density meter, was found to be 1.05*103
kg/m3. Figure 3.2 shows a SEM photograph of the PS-particles. The
surface roughness of the particles was in the order of 0.07 to 0.6% of the particles
radius (see section 5.4.3).
Amorphous
silica
(Si02) dispersion
Silica (Si02)-spheres were prepared by the method of Tan et al. [9]
at -20 ° C in a 10 litre vessel gently stirred with a magnetic stirrer.
N-propanol (Fluka AG) was used as a solvent. Tetramethylorthosilicate (98%,
Janssen Chimica) was distilled before use. The mixture was kept at -20 °
C for 16 hours. The particles in the silica dispersion had a number averaged
diameter of 1.705 m m. Their volume averaged diameter was 1.799 m m. The particle
sizes were determined with the Coulter LS-130. The density of the silica, as
measured by means of a Quantachrome stereo pycnometer, was found to be 2.00*103
kg/m3. Figure 3.3 shows a SEM photograph of the silica particles.
Quartz
dispersion
Quartz (Merck p.a.) was ground in
ethanol in an agate ball mill for 24 hours. After decanting and drying the solid
was dispersed in twice distilled water and fractionated by sedimentation. The
quartz dispersion had a number averaged diameter of 1.934 m m. Their volume
averaged diameter was 2.290 m m. The particle sizes were determined with the
Coulter LS-130. The density of the quartz, as measured by means of a Quantachrome
stereo pycnometer, was found to be 2.67*103 kg/m3. The
quartz particles were not spherical. Figure 3.4 shows a SEM photograph of the
quartz particles.

Figure 3.2: SEM photograph of the polystyrene particles (L-93).
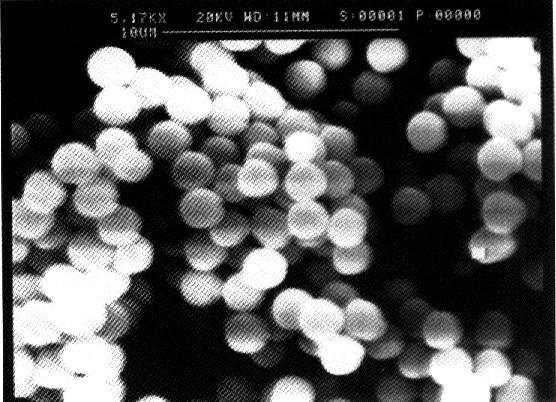
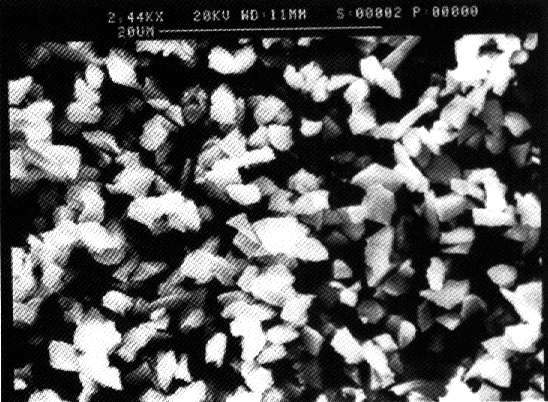
Figure 3.4: SEM photograph of the quartz particles. Materials Densities between polystyrene and aqueous solutions were matched (resp. nearly matched) by addition of deuterium oxide (ex. Merck, nr.2919). Matching of densities is not possible in the case of amorphous silica and quartz dispersions since the density differences between amorphous silica or quartz and water are too large.
Determination
of solids contents
The solids percentage of the
polystyrene latex was determined by drying a known amount of the dispersion
in an oven at 105 ° C, until constant weight was reached.
Procedure
of the µg experiments
Coagulation
experiments were performed at a volume fraction of 1*10-4, except
those with the silica dispersion which were performed at a volume fraction of
3*10-4. This is because the refractive index of silica is 1.498 and
the concentration of particles has to be increased in order to obtain a similar
light intensity (at t=0) as in the case of the other dispersions. Suspensions
with twice the mentioned concentrations, were prepared by diluting a concentrated
dispersion with twice distilled water, using ultrasonic vibrations for dispersing
(by means of a Branson 1200 Ultrasound Bath). 10 ml of this dispersion was mixed
with an equal volume of a 1 M NaCl solution, with the chemical added for (nearly)
matching densities.
During lift-off the rocket rotates around its axis. The spin is stopped when
the rocket reaches its maximum height. When the spin and the stirrer of the
coagulation vessels are stopped, the fluid in the vessels may still rotate during
a certain time. Krutzer [1] checked how long this residual fluid motion lasts.
He concluded that the time required for the fluid to come to rest does not exceed
a period of 22 seconds. Because the time between the stopping of the spin and
the start of the experiment is 25 seconds, no influence is expected.
Because the rocket can only be launched if the weather conditions are good,
it may happen that the dispersion has to be kept for several days in the module,
before the actual µg experiment takes place. In order to check whether the coagulation
behaviour changes if the dispersion is preserved during a week, experiments
were performed in which a dispersion was homogenized every 24 hours after which
a coagulation experiment was carried out, during a period of nine days.
After being filled completely, the vessels were closed and vacuum tests were
made to check for air bubbles. This procedure was repeated a few times until
all the vessels were free of air bubbles. At last all vessel were subjected
to ultrasonic vibration for two minutes in order to check if any air bubbles
would appear. If their presence was suspected, the filling and closing procedure
was repeated until all the vessels were free of air bubbles. Air bubbles must
be excluded because they may disturb the measurements at µg conditions.
The µg experiments were performed in 10 vessels and the vessels were divided into two groups of five vessels each: group`A' and group`B'. Table 3.1 shows a time schedule of the launching.
|
Table 3.1: The time schedule |
|
|
time (s) |
TEXUS 31 |
|
-800s |
All lasers ON |
|
-780s |
Ultrasound and Motor ON |
|
-630s |
1g-reference:Mixing A and B OFF |
|
-280s |
Ultrasound, Motors, Laser ON |
|
-240s |
Program begin Visualize:Ultrasound and Motor ON |
|
-70s |
Mixing: Ultrasound and Motor ON |
|
-20s |
Laser OFF |
|
±0s |
Lift Off |
|
+55s |
Laser Cell 1-10 ON |
|
+80s |
µg -Experiments Group A:Mixing A OFF µg -Experiments Group B:Mixing B OFF |
|
+430s |
Everything OFF |
|
+440s |
Timer Stop |
A short time before the rocket was launched (± 30 minutes) a 1g reference experiment was performed in every experimental unit in the module, then the rocket was launched. During lift-off, the ultrasonic suspender and the stirrer were switched on, to prevent sedimentation and aggregation. Ultrasonic vibrations and stirring were switched off a few seconds after µg conditions had been reached.
The reference experiments were performed at 20 ° C. During the flight the temperature inside the module (the temperature detectors were placed outside the vessels) increased to 26 °C.
Data acquisition
During the flight, the
data of the coagulation experiments, were sent by means of telemetry to a computer
at the launch base. The slopes of the light intensity versus time plots, were
calculated by the procedure of linear regression.
3.3 Results & Discussion
The launching of the rocket turned out to be prosperous, all ten experimental units functioned well and the module was not damaged during the flight.
The experiments in which the influence of the waiting time was studied, showed that during a period of nine days, no significant change in coagulation behaviour was found for the polystyrene, quartz and silica dispersions.
The results of the µg experiments are shown in figures 3.5 to 3.9; all the figures show the light intensity (in arbitrary units) vs. time plots for the 1g reference experiment and the experiment at µg conditions.
In the discussion, short-time fluctuations are distinguished from long-term changes of slope; in all cases, at least part of the curves could be represented as a linear curve with short-time fluctuations superimposed on it. We will refer in those cases to a linear (part of the) curve.
Figure 3.5 shows the results for L-93 (no chemicals added to match densities), with a density difference of -31 kg/m3 (D r =r medium-r disperse phase). One can see a pronounced increase in coagulation rate at µg conditions compared with the experiment at 1g. These results show also, that during and shortly after lift off, the dispersion was homogenized very well, because the light intensities right at the start of the experiments are the same for 1g and m g conditions.
The results for L-93, with a density difference of 1 kg/m3 (deuterium oxide added to match the density), are shown in figure 3.6. Here also an increase in coagulation rates was observed which was not expected. It can also be seen that the homogenizing procedure during lift off, was not so good as in the case of the dispersion with a density difference of -31 kg/m3; in the micro-gravity case, the light intensity is slightly higher at the beginning of the experiment compared to the 1g case.
Figure 3.7 shows the results for L-93, density difference 29 kg/m3. The results are very similar to those for the dispersion with a density difference of -31 kg/m3.
Figure 3.8 shows the results of the quartz dispersion. Here also one can see an increase in coagulation rate but the increase is less pronounced than in the polystyrene dispersions.
The results of the silica dispersion are shown in figure 3.9. As with the quartz dispersion, one can see an increase in coagulation rate which is less pronounced than in the polystyrene dispersions.
Figure 3.5: Light intensity vs. time, density difference -31 kg/m3 (no chemicals added to match the densities), L-93 (polystyrene), 1g and µg .
Figure 3.6:
Light intensity vs. time, density difference 1 kg/m3 (deuterium oxide
added to match the densities),
L-93 (polystyrene), 1g and µg .

Figure 3.7: Light intensity vs. time, density difference 29 kg/m3 (deuterium oxide added to match the densities), L-93 (polystyrene), 1g and µg .
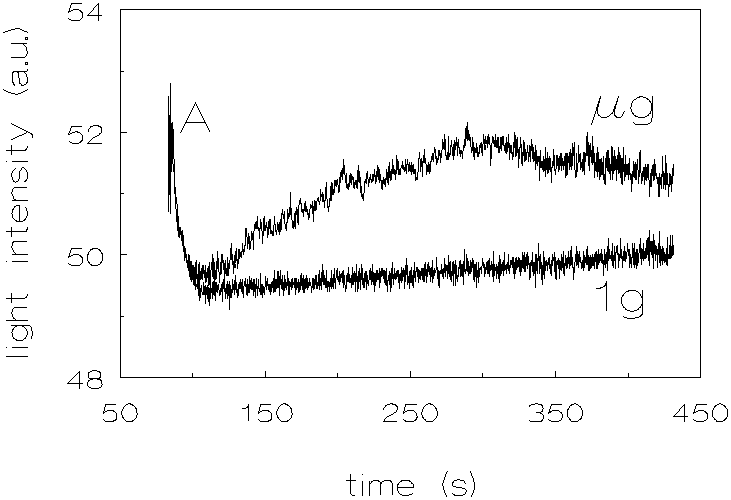
Figure 3.8: Light intensity vs. time, no chemicals added to match the densities, quartz, 1g and µg .
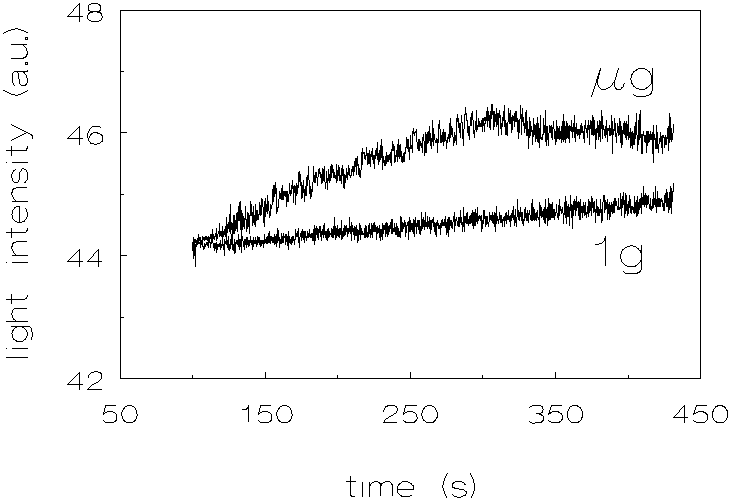
Figure 3.11: Light intensity vs. time, no chemicals added to match the densities, silica, 1g and µg .
In discussing the results it is difficult to compare the coagulation rates quantitavely; light intensities were measured instead of light transmission and the experimental units are not exactly identical, in addition the particle concentrations of the silica dispersions were different. Nevertheless, some comparisons can be made.
The difference between coagulation rates for the polystyrene dispersions with a density difference of -31 kg/m3 and 29 kg/m3, at µg conditions compared with 1g conditions, is about the same. The difference in increase in light intensity with time at µg conditions, compared with 1g, is in the case of D r =1 kg/m3 about twice as large as in the cases of D r =-31 kg/m3 and D r =29 kg/m3. It was not expected, that the coagulation rate for the dispersion with a density difference of 1 kg/m3, would increase at µg conditions, compared to 1g conditions.
Probably it is not possible to match the densities of the continuous phase and the dispersed phase at 1g, exactly. One explanation for the difference in coagulation rate is that the separate particles have different densities; a difference of 1 kg/m3 must be considered to be small but significant. Another explanation is free convection due to small temperature gradients caused by temperature changes in the surroundings. This type of convection is not operating at µg -conditions. At 1g this type of convection may disrupt formed doublets of particles (see chapter 5.6).
When looking at the results of the quartz dispersions, it can be noticed that at the beginning of the coagulation experiments (A in figure 3.8), there is a steep decrease of the light intensity. This phenomenon can be explained by the fact that the non-spherical quartz particles align themselves during stirring. When the stirring is stopped, the light intensity is found to decrease because the particles will take in a random orientation. The light intensity at time t=0 was taken to be the one after the decrease. The increase in coagulation rates, at µg conditions, compared to 1g conditions, for the quartz dispersions is less pronounced than for the polystyrene dispersions (the proportionality coefficient CEN of section 2.2 taken into account, as determined by Krutzer [1], which is for quartz 4.62±0.32 and for polystyrene 3.71±0.24). This difference can be explained by the fact that the quartz particles are non-spherical. The deviation of the spherical shape may result in a decrease in hydrodynamical resistance when two particles approach each other; the last liquid film between two approaching particles can be pierced by angular protrusions. The silica dispersions show also an increase in coagulation rates at µg conditions, compared to 1g conditions. However, because these experiments were performed with a particle volume fraction of 3 * 10-4, the results can not be quantitatively compared with the other dispersions.
The form of the transmission versus time curves is different under µg than under 1g-conditions. Under µg conditions the curves are convex toward the time axis. Under 1g-conditions a linear curve (upto t » 300 s) and as time is proceeding a more concave curve toward the time axis can be observed. The explanation of the different character of the curves at 1g and µg conditions is that at 1g-conditions there is aggregation and aggregate disruption while at µg conditions the disruption term is less operative. This explanation is confirmed by analysing the detection signals; at 1g the signal fluctuates many times per unit of time. These fluctuations (see figure 2.3 and the figures in the present chapter) are not caused by noise of the detection signal, but should be ascribed to a continuing process of aggregation and disruption of particles. This was checked by registrating the signal of pure water and of a non-coagulating dispersion. At µg the disruption is less distinct causing a steep increase of the signal at the beginning of the coagulation process, resulting in a convex curve. This can be seen when analysing the signals at µg conditions: there are much less fluctuations per unit of time. We have quantized this with the calculation of the autocorrelation function; the results of the calculations are shown in Figure 3.12.
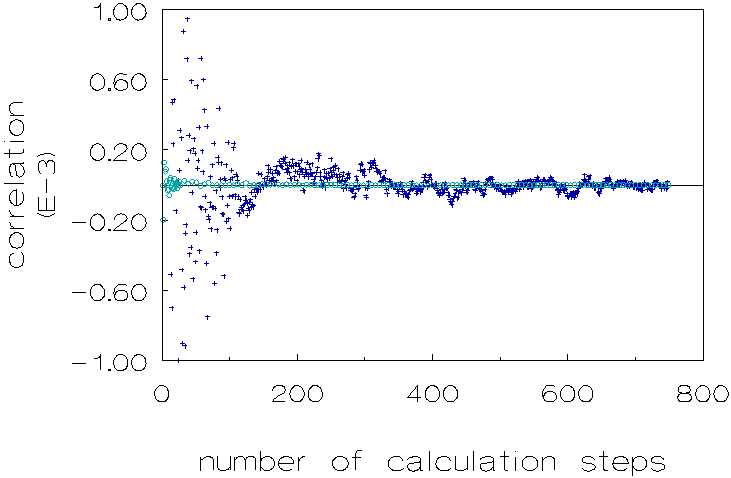
Figure 3.12: Autocorrelation function of transmitted light intensity for 1g (¡ ) and µg (+) conditions, over a time period of 165 seconds. Polystyrene dispersion in 0.5 M NaCl solution, unmatched density.
This figure is based on the data of figure 3.7 by substracting from the values in the latter figure, values obtained from a linear interpolation between the data in the same figure, based on the minimum x2 criterion (x: deviation of measured value from the linear interpolation value). Both calculations of the autocorrelation functions were performed over a time period of 165 seconds, in which 750 measurements were recorded.
Figure 3.12 shows that there is a distinct difference in correlation when comparing 1g and m g conditions.
The levelling off, of all the light intensity curves during coagulation at 300-350 seconds can be explained by three possible explanations:
1. Aggregates formed after 300-350 seconds have dimensions for which the light intensity is not increasing any more but starts to fluctuate (see also figure 2.5).
2. At the end of the µg experiment (t » 300 s), gravity is increasing causing the levelling off of the signal.
3. Decrease of the amount of primary particles.
The results of our coagulation experiments show a higher coagulation rate at µg than at 1g conditions. These results are very interesting, since theory appears to lead to the reverse expectation [10,11]. The mutual influence of Brownian and gravity induced motion on coagulation rate, was studied by Melik and Fogler [10], who performed calculations of the coagulation rate in the case of low Pegr-numbers. Additional calculations were performed by Wang and Wen [11]. It was concluded that for these small Pegr-numbers gravity induced motion always increases the Brownian coagulation rate. In the case of larger Pegr-numbers, calculations on the rate of coagulation were done by Wen, Zhang and Lin [12]. They found that Brownian diffusion may decrease the coagulation rate.
At the moment, four phenomena seem to be feasible to explain the results;
a): hydrodynamics: the non-linear terms in the Navier-Stokes equations may become important when two particles are close, even at small Re-numbers;
b): streaming potentials during sedimentation and mutual approach of two particles;
c): interaction potentials in combination with the surface roughness of the particles;
d): free convection due to small temperature gradients caused by temperature changes in the surroundings, causing a disruption of formed doublets at 1g.
These phenomena will be discussed in chapter 5.
3.4 Conclusions
The main conclusion of this chapter is that coagulation rates for dispersions of polystyrene, quartz and silica are significantly larger at µg conditions than at 1g. Even the polystyrene dispersion, with a density difference of 1 kg/m3, showed a difference between µg and 1g coagulation rates. One explanation for this is that at 1g, the densities of the continuous phase and the dispersed phase, cannot be matched perfectly. This implies that in the case of polystyrene there are differences in density between various particles; the differences may be small but significant. Density differences between various particles indeed have been experimentally found. Another explanation is free convection due to small temperature changes.
At 1g doublets of particles are disrupted. This is not only concluded from the slopes of the light intensity versus time curves but also by analysing the form of the curves. At 1g many fluctuations of the signal per unit of time (aggregation and disruption of particles) compared with the signal at µg (aggregation and much less disruption), resulting in a linear curve at 1g and a convex curve at µg . This difference in the curves (1g and µg ) is also confirmed when calculating the autocorrelation function for both curves; there is a distinct difference in correlation when comparing the two curves.
References
(1) Krutzer, L.L.M.,
The Influence of Flow Type, Particle Type and Gravity on Orthokinetic
Coagulation, 1993, Ph. D. Thesis, Eindhoven University of Technology.
(2)
van Diemen, A.J.G., Stein, H.N., J. Colloid Interface Sci., 1983,
96, 150.
(3)
Logtenberg, E.H.P., The Relation between the Solid State Properties
and the Colloidal Chemical Behaviour of Zinc Oxide, 1983, Ph.
D. Thesis, Eindhoven University of Technology.
(4)
Brakalov, L.B., Chem. Eng. Sci., 1987, 42, 2373.
(5)
van de Ven, T.G.M., Mason, S.G., Colloid Polym. Sci., 1977,
255, 794.
(6)
Zeichner, G.R., Schowalter, W.R., Assoc. Ind. Chem. Eng. J., 1977,
23, 243.
(7)
Tuin, G., Peters, A.C.I.A, van Diemen, A.J.G., Stein, H.N., J. Colloid
Interface Sci., 1993, 158 (2), 508.
(8)
van de Hulst, H.C., Light Scattering by Small Particles, Dover
Publications, Inc., New York, 1981, chapter 9.
(9)
Tan, C.G., Bowen, B.D., Epstein, N., J. Colloid Interface Sci.,
1987, 118, 290.
(10)
Melik, D.H., Fogler, H.S., J. Colloid Interface Sci., 1984,
101, 84.
(11)
Wang, Y.G., Wen, C.S., J. Fluid Mech., 1990, 214,
599.
(12)
Wen, S., Zhang, L., Lin, H., J. Colloid Interface Sci., 1991,
142, 257.