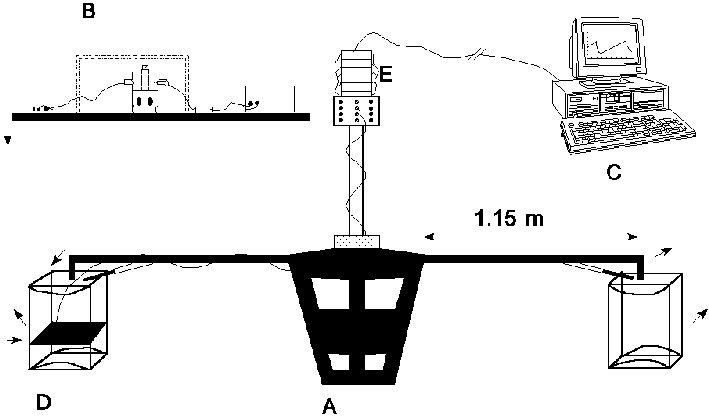
Figure 4.1: Schematic representation of the AMC centrifuge experiment, with A: rotating drive system, B: coagulation apparatus, C: computer and measuring system, D: swing basket, E: contact slip rings. (Click picture for more detail)
Chapter 4
PERIKINETIC COAGULATION AT 1G AND HIGH-G CONDITIONS
Abstract
In this chapter, experiments on perikinetic coagulation of polystyrene dispersions are described which were performed at 1g and high-g conditions in a centrifuge. Experiments were performed at 1g, 2g, 4g and 7g, with different densities of the continuous phase; also a mixture of two different polystyrene latices was used (d1 » 1 m m and d2 » 3 m m). The results of the high-g experiments show that the most pronounced effect of gravity on coagulation rate is found for dispersions with a small density difference, on going from 1g to 2g. In this regime a significant decrease in coagulation rates is observed. For higher g-levels, no change, or an increase in coagulation rate is observed. For the latex-mixture at pronounced density differences, gravity induced coagulation was observed; however the formed doublets did not have a lasting contact. From calculation of the bulk forces acting on the particles, it was found that the detachment force for the larger particle of the formed doublet is in the order of 10-14 N. The rate constant calculated at m g-conditions approaches the theoretical value of von Smoluchowski. By means of a video analysis of the perikinetic coagulation process, the formation of doublets was studied for a density difference of D r =-31 kg/m3 and D r =1 kg/m3. It turned out the the `interaction time' for two particles was longer for the density matched dispersion. In general it was concluded from the analyses that doublets of particles are easily disrupted and that at 1g, free convection currents were observed even at small temperature differences in the system.
4.1 Introduction
Among others, Krutzer [1] studied the influence of flow
type, particle type and gravity on orthokinetic coagulation. Before Krutzer,
Van Diemen and Stein [2], Logtenberg [3] and Brakalov [4], performed shear induced
coagulation experiments under 1g conditions. As mentioned in chapter 3, their
experiments showed a slower coagulation than theoretically expected and conclusions
from these experiments were uncertain because of the interplay of several factors;
the changed attraction as a result of deviations of the particle shape from
a spherical shape, the complicated nature of the flow pattern in the experimental
set-up, the role of inertia and the interplay of Brownian, shear-induced and
gravity induced coagulation. As mentioned in chapter 3, Van de Ven and Mason
[5] and Zeichner and Schowalter [6], performed theoretical calculations which
all refer to spherical particles in the absence of inertia. Coagulation is impossible,
when there is no interaction between two particles. The trajectories (see also
section 3.1) of the particles can be divided into `open' and `closed' ones,
separated by a `limiting' trajectory; in the absence of interparticle forces
it is impossible for a particle to cross a limiting trajectory. However, when
attractive London-Van der Waals forces are operative, it is possible for an
approaching particle to cross the limiting trajectory and coagulation can occur.
In chapter 3 we also discussed that Logtenberg [3] concluded from his trajectory
calculations that for spherical particles with a radius of 10-7 m
to 10-6 m, inertia forces do not play a role of importance.
In order to get a better understanding of the inertia forces and the interplay
of gravity and Brownian-induced coagulation, we performed in addition to the
µg experiments described in chapter 3, perikinetic
coagulation experiments at 1g and high-g conditions.
One way to study the influence of gravity on coagulation, is to change the density
of the continuous phase of a dispersion. Hofman [7], carried out coagulation
experiments of decane-CCl4 emulsions, stabilized by AOT (Aerosol
OT, commercial surfactant) in NaCl-solutions. By varying the CCl4
concentration, he was able to influence the density of the disperse phase. He
also found a maximum coalescence rate at D r
=0, but this is not really conclusive evidence because on changing the
CCl4 concentration a number of factors change (interfacial tension
etc.).
In adapting the density of the continuous phase, one can establish a density
difference between the continuous phase and the dispersed phase; when the density
of the dispersed phase is higher, the particles will settle, when the density
is lower, the particles will rise (creaming). When the densities of the dispersed
phase and the continuous phase are exactly the same, the particles will float
in the fluid. With respect to the sedimentation behaviour this is a simulation
of µg conditions.
In the present chapter polystyrene (L-93) was used as the dispersed phase, which
has a small density difference with the continuous phase (aqueous solution).
The density of the aqueous phase can be changed by adding sucrose, methanol
or deuterium oxide. Sucrose and methanol were used because they do not induce
surface charges, but a disadvantage is that the viscosity of the continuous
phase is changed. That is why also deuterium oxide was used because in this
case no correction needs to be applied for viscosity changes. With sucrose and
deuterium oxide it is possible to match the densities of the continuous phase
and the dispersed phase, if the latter is polystyrene.
In order to study the influence of gravity on the system discussed above, also
a series of experiments were done at different g-levels, by means of a centrifuge,
located in Amsterdam at the Academical Medical Centre. In the centrifuge, experiments
were performed at 1g, 2g, 4g and 7g. Not only a latex with d=1.879 m
m was used, but also a mixture (1:1 by volume), of two polystyrene latices with
d=1.288 m m and d=3.230 m
m was used.
Because of problems with the power supply (disturbances of the power signal,
caused by the contact slip rings of the centrifuge), a I/V-converter had to
be implemented. This apparatus filters the signals between the centrifuge and
the measuring computer. An additional problem with this apparatus was that the
quantitative results of the coagulation rates at 1g, were slightly different
from those found in the laboratory. Therefore also 1g experiments were done
in the centrifuge, as reference for the higher g experiments.
4.2 Experimental
Polystyrene-latex
The method for the preparation of the polystyrene latices is described in [8].
Particle sizes were determined by means of the Coulter LS-130 (see section 3.2).
The density, as measured by means of a Paar DM A-10 density meter, was found
to be 1.05*103 kg/m3. The surface roughness of the particles
was in the order of 0.07 to 0.6% of the particle radius (see section 5.4.3).
The first polystyrene latex particles (L-93) used for these experiments had
a number averaged diameter of 1.879 m m. (see
for the codes of the various polystyrene dispersions section 2.2). The volume-averaged
diameter was 2.030 m m. The second latex used
was a mixture of latex L-86 and L-89 (1:1 by volume, indicated as L-86/L-89,
volume fraction 10-4). Latex L-86 had a number averaged diameter
of 1.288 m m and the volume-averaged diameter
was 1.362 m m. Latex L 89 had a number averaged
diameter of 3.230 m m and the volume-averaged
diameter was 3.308 m m.
Materials
Densities between polystyrene and aqueous solutions were matched (resp. nearly
matched) by addition of sucrose (ex. Janssen Chimica, p.a.), methanol (ex.
Merck, p.a. nr.5868) and deuterium oxide (ex. Merck, nr.2919). Of all solutions
used, densities were measured by means of a Paar DM A-10 density meter and
kinematic viscosities by means of a AVS-310 viscosimeter.
Determination of solids contents
The solids percentage of the polystyrene latices were determined by drying a
known amount of the dispersion in an oven at 105 °
C, until constant weight was reached.
Viscosity measurements
The viscosities of the continuous phases were determined in a capilarry
viscosity meter [9]. Experiments were performed at T=22 °
C.
Procedure of the 1g and high-g experiments
The suspensions for the coagulation experiments were prepared in the same way
as described in section 3.2. All 1g-experiments were performed in the apparatus
shown in figure 2.2. The experiments at high-g conditions were performed in
a centrifuge as shown in figure 4.1, at 20 ± 1 °
C. The experimental set-up as used for the 1g experiments was placed in the
swing basket of the centrifuge. As reference a 1g experiment was done and after
that, the centrifuge was started. During the start-up procedure, the stirrer
and the ultrasonic disperser were switched on. When the desired g-level was
reached, the stirrer and the ultrasonic disperser were switched off and the
coagulation experiment started. After about twenty minutes the experiment was
finished, and the stirrer and the ultrasonic disperser were switched on again
till constant extinction (corresponding to the start value of E0)
was reached. Then a higher g-level was chosen to perform the next experiment,
with the same procedures as described above. Temperature fluctuations in the
swing basket were in the order of 1-2 ° C. All
cycli (from 2g till 7g) were done in duplicate, with newly made dispersions.
Four groups of experiments were done, differing both in dispersed phase and
in chemicals added for (nearly) matching the densities:

Figure 4.1: Schematic representation of the AMC centrifuge experiment, with A: rotating drive system, B: coagulation apparatus, C: computer and measuring system, D: swing basket, E: contact slip rings. (Click picture for more detail)
1) Polystyrene L-93, sucrose or methanol;
2) Polystyrene L-86/L-89, sucrose or methanol;
3) Polystyrene L-93, D2O;
4) Polystyrene L-86/L-89, D2O.
Data acquisition
During the coagulation experiments, all the data were collected by a personal
computer. The slopes of the light transmission versus time plots, were calculated
by the procedure of linear regression. The regression was restricted to the
linear part of the curves (i.e. the part without long-term change of slope).
Heraeus centrifuge experiments
In order to check whether the density of separate PS-particles varies,
we performed also some experiments in a centrifuge (Heraeus ES 3000 IKS). The
experiments were performed with L-93 (D r
=1 kg/m3), density matched with deuterium oxide, at 800 g. See also
footnote 1 in chapter 3, page 48.
4.3 Results & Discussion
1g-experiments (L-93)|
Number |
r *103 (kg/m3) |
D r (kg/m3) |
h *10-3 (Pa*s) |
h /h water*dlnE/dt (10-6 s-1) |
|
1 |
1.112 |
62 |
2.09 |
3.03 |
|
2 |
1.081 |
31 |
1.54 |
3.48 |
|
3 |
1.066 |
16 |
1.37 |
5.49 |
|
4 |
1.060 |
10 |
1.31 |
6.34 |
|
5 |
1.049 |
-1 |
1.23 |
7.55 |
|
6 |
1.040 |
-10 |
1.14 |
6.14 |
|
7 |
1.035 |
-15 |
1.10 |
5.19 |
|
8 |
1.029 |
-21 |
1.07 |
4.25 |
|
9 |
1.019 |
-31 |
1.02 |
3.43 |
|
10 |
0.988 |
-62 |
1.65 |
3.17 |
|
11 |
0.972 |
-78 |
1.78 |
3.13 |
|
12 |
1.051 |
1 |
1.02 |
6.39 |
|
13 |
1.098 |
48 |
1.02 |
3.49 |
1g experiments (L-86/L-89)
Values of the densities and viscosities for each dispersion
are the same as presented in Table 1. Figure 4.3 shows the coagulation rate
as a function of the density difference, after correction had been made for
viscosity differences.
Going from a small density difference to a density difference of almost zero,
one can see an increase in coagulation rate by a factor »
2. Again there is no significant difference in this respect, between experiments
with a continuous phase with lower density than that of the disperse phase and
experiments in which the density of the continuous phase is higher than that
of the disperse phase.
The absolute values for the coagulation rates are higher for the polydisperse
system (L-86/L-89) than for the monodisperse system (L-93). There are two reasons
for this result: i) The particle concentration for the polydisperse system is
higher and ii) the Brownian-coagulation rate is higher for initially polydisperse
than monodisperse particle size distributions [10,11,12].

Figure 4.2: Coagulation rate as a
function of the density difference for L-93 at 1g, with n
methanol, Ù sucrose, l
D2O, to adapt the densities of the continuous phases.
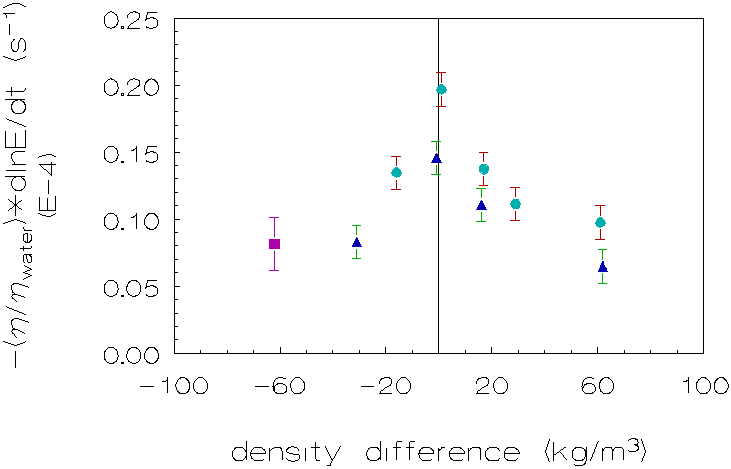
Figure 4.3: Coagulation rate as a function of the density difference for L-86/L-89 at 1g, with n methanol, Ù sucrose, l D2O, to adapt the densities of the continuous phases.
The difference in coagulation rate between
the density matched dispersion and the situation when there is a pronounced
density difference between the dispersed and continuous phase, is contrary
to theoretical expectation. Theories on coagulation (chapter 2 and chapter
3), usually assume the absence of such an influence; and if any such influence
is found, the evidence concerned should be checked as to whether the experiments
are disturbed by incomplete fulfilment of assumptions made either explicitly
or not, in calculating the coagulation rate from the data. The data obtained
in the present investigation all go back to light transmission vs. time
measurements. Experimental coagulation rates as reported here increase with
vanishing density difference between disperse and continuous phase. Disturbance
of the interpretation of light transmission as measure of coagulation rate,
by the presence of a gravity field or of a density difference, would act
in the reverse direction: i) Different settling rates bring particles into
each other's vicinity that would remain apart in the absence of a gravity
field (when Brownian motion can be neglected); this would increase the coagulation
rate, ii) such different settling rates induce additional shear which superimposes
a shear-induced coagulation on the Brownian coagulation, iii) in the presence
of a gravity field, coagulation measurements by light transmission might
be disturbed by sedimentation.
Part of the suspended solids may be removed by sedimentation from that part
of the coagulation vessel which is passed through by the light beam; thus
light transmission would increase faster than when this effect would be
absent. This also would increase the apparent coagulation rate rather than
decrease it. Nevertheless, the present investigation shows that the reverse
is found.
High-g experiments
The results of the high-g experiments are
shown in the figures 4.4-4.7.
First group (L-93, matched with sucrose/methanol;
figure 4.4)
The problem with methanol as matching agent was that the data could
not be reproduced very well. This is not surprising, since methanol has
a lower dielectric constant than water (78.54 vs. 32.63) and according to
Verdegan et al. [13] methanol is expected to adsorb at the latex-water interface.
These phenomena will have an influence on the electrophoretic properties
and the interaction energies of the particles.
Looking at Figure 4.4 one can see that for small density differences the
coagulation rate is decreasing, while for larger density differences no
significant change, or in some cases a slight increase, in coagulation rate
was observed. The decrease in coagulation rate is most pronounced going
from 1g to 2g.
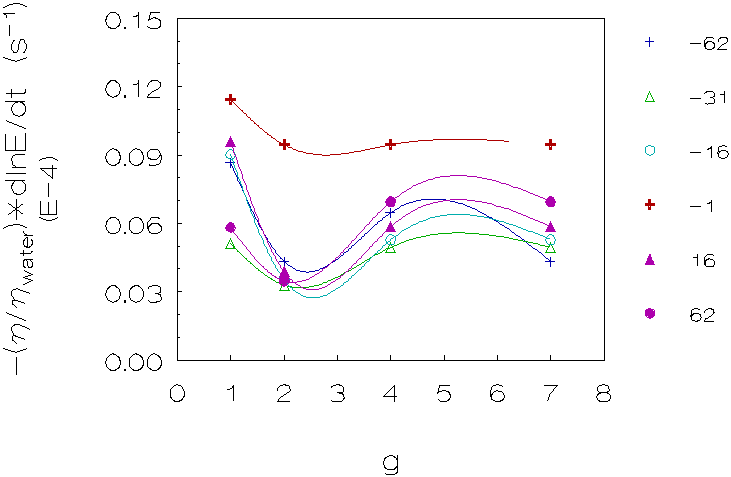
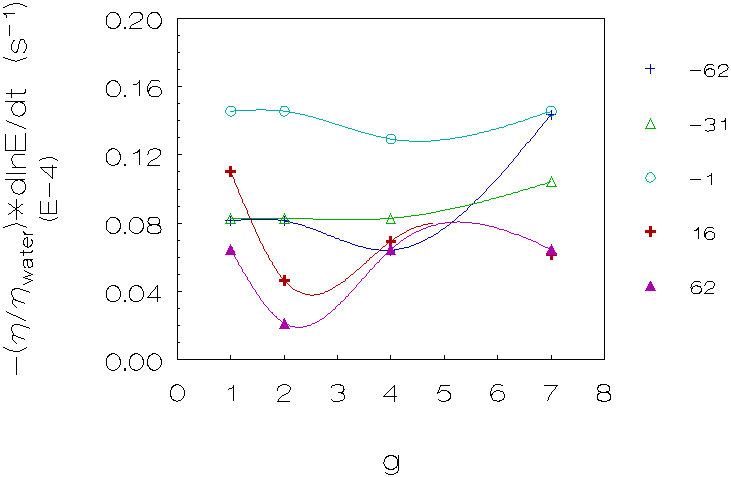
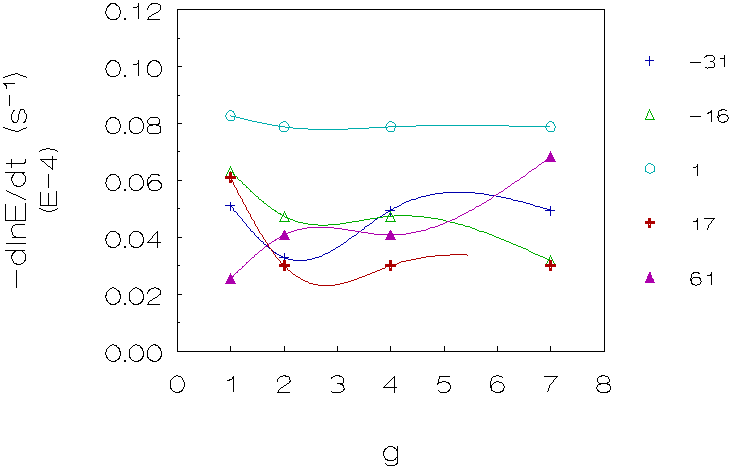
Figure 4.6: Coagulation rate vs. g for 5 density differences (kg/m3), L-93 (densities matched with deuterium oxide). The curves are just a guide to the eye.
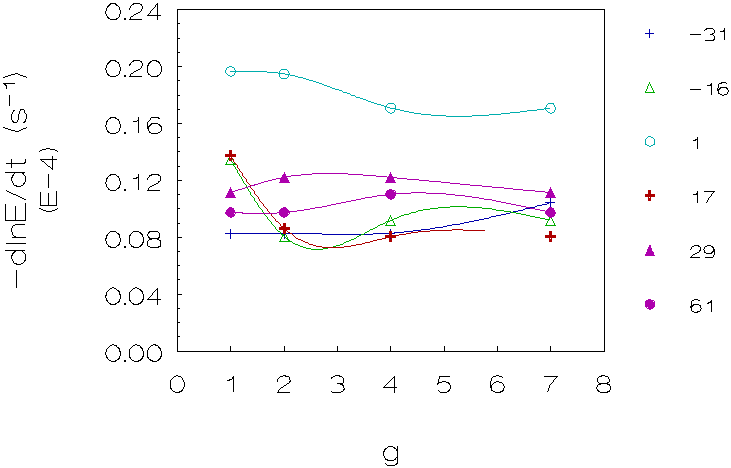
Figure 4.7: Coagulation rate vs. g for 6 density differences (kg/m3), L-86/L-89 (densities matched with deuterium oxide). The curves are just a guide to the eye.
Second group (L-86/L-89, matched with sucrose/methanol;
figure 4.5)
Once again, problems are encountered with reproducing
the experimental data of the dispersions matched with methanol. For this
group of measurements, one can also observe a decrease in coagulation rate
for small density differences, at higher g-levels an increase in coagulation
rates can be observed.
Third group (L-93, matched with deuterium oxide;
figure 4.6)
These results also show in the majority of cases a decrease in coagulation
rates for small density differences, going from 1g to 2g, however the increase
in coagulation rates for larger density differences going from 2g to higher
g-levels is more pronounced.
Fourth group (L-86/L-89, matched with deuterium
oxide; figure 4.7)
These measurements show in the majority of cases a decrease in coagulation
rates going from 1g to 2g for small density differences and no change or
a small increase for larger density differences going from 2g to higher
g-levels. Please note that the slope for these measurements was taken before
the steep increase of the light intensity, caused by gravity induced coagulation
(see also figure 4.8).
Heraeus centrifuge experiments
The vessel with the polystyrene dispersion showed a fraction of particles
which was sedimented, a fraction which was creamed and a fraction which
was still floating in the liquid. So obviously the density of the separate
particles varies: there is a fraction of particles with a density of 1.05
kg/m3 (as was measured) but also a small fraction of particles
with a lower density and a small fraction of particles with a higher density.
See also footnote 1 in chapter 3, page 48).
In general, the error of the experimental transmitted
light intensity data is about 5-10%, which correpsonds to ± 5*10-7
s-1 in the dlnE/dt values. The results obviously could not always
be reproduced very well. Nevertheless, the results can be summarized as
follows: the most pronounced effect of gravity on the coagulation rate is
found for small density differences, going from 1g to 2g. For higher g-levels
no distinct influence or an increase in coagulation rate is observed.
There are two possible explanations for this increase in coagulation rate
for larger density differences at higher g-levels:
i) Gravity induced coagulation forms doublets of particles which sediment
faster than single particles. This phenomenon is expected especially at
larger density differences and high g-levels (see also section 4.4),
ii) At higher g-levels the swing basket of the centrifuge takes in a more
horizontal position. In the more horizontal position, the centrifugal acceleration
is becoming more important and causes a gravity gradient (»
0.8 g) along the glass vessel (the particles at the top of the vessel are
less accelerated than the particles at the bottom of the vessel). This gradient
in acceleration causes a gradient in particle concentration. This means
that the increase in light intensity is not only caused by coagulation,
but also by the fact that the particle concentration decreases by sedimentation,
at the measuring spot in the middle of the vessel.
The mutual influence of Brownian and gravity induced motion on coagulation rate, was studied by Melik and Fogler [13], who performed calculations of the coagulation rate in the case of low Pegr-numbers. Additional calculations were performed by Wang and Wen [14]. It was concluded that for these small Pegr-numbers gravity induced motion always increases the Brownian coagulation rate. In the case of larger Pegr-numbers, calculations on the rate of coagulation were done by Wen, Zhang and Lin [15]. They found that the gravitational capture efficiency is decreased by Brownian diffusion only when the gravity induced relative motion dominates over the interparticle potential induced motion. In a flow field Brownian diffusion will transfer a sphere j from the upstream area along the streamlines into the downstream area, from where it will be convected downstream further by the convection induced by gravity without collection by sphere i. They concluded that this is a process which interacts closely with the strength of the basic flow. In agreement with the results of chapter 3, the results reported in the present chapter show an increase in coagulation rate as D r becomes smaller; in addition a decrease in coagulation rate is found when the g-level becomes higher.
4.4 Gravity induced coagulation
For the latex-mixture the following behaviour was observed
at the highest density differences; i) a sudden increase in light transmission
followed by ii) a sudden decrease of the light transmission. The initial
dlnE/dt-value was calculated from the slope before the peak in section
4.3.
As can be seen from the graph, in figure 4.8,
the peaks occur at shorter times when gravity is increased. In addition
the peaks become more pronounced. This behaviour indicates a gravity induced
coagulation mechanism, which can be understood as follows: larger particles
sediment faster than the smaller particles, at some point in the process
the larger particles will catch the smaller ones. This is illustrated in
Figure 4.9.
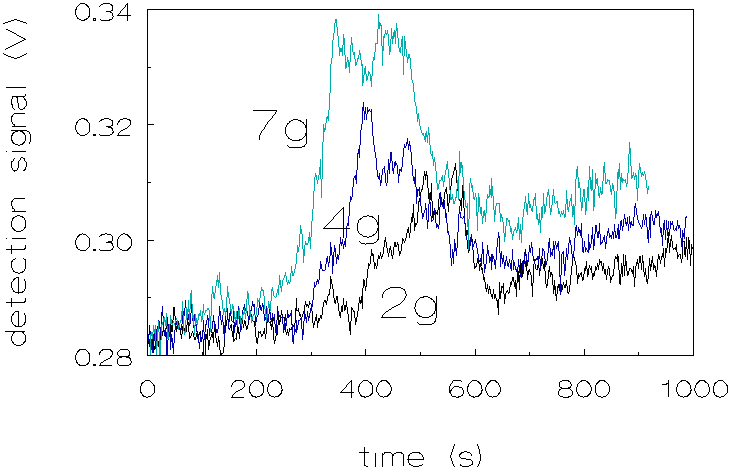

Figure 4.9: Mechanism of the gravity induced coagulation process. The larger particles catches the smaller one (light transmission increases), then the formed doublet will rotate. Depending on the interaction forces, the particles will either sediment as a doublet or the larger particle will detach from the smaller one.
As the g-level increases the particles sediment faster and the peak will appear at shorter time scales. At higher g-levels also the intensity of the peak increases. This can be explained as follows: when larger particles sediment faster, there are more successful collisions to form a doublet, because both the frequency of occurence and the effectiveness of the collisions increases. The lifetime of the formed doublets apparently is short because light transmission decreases again after the doublets are formed. Obviously the attractive interaction energies in most cases are not strong enough to ensure a lasting contact. However, the gravity-induced formation and subsequent disruption of pairs of particles, 3 m m and 1 m m in diameter, can explain the increase of light transmission at the start of the peak, but not the decrease, since particles from disrupted pairs will again form new pairs with different partners. Therefore gravity-induced particle pair formation and disruption would lead to an increase in light transmission followed by a constant level of intensity of transmitted light when a stationary state is reached. Appearance of a peak (with decrease of the transmitted light at its backside) indicates that during the ca. 200 sec. of the peak, conditions in the coagulating system change such as to prevent further gravity-induced coagulation. Two factors have been envisaged which might change during the time concerned:
a) The gravity-induced coagulates concerned are so large
that they are removed from that spot of the system where light transmission
is measured;
b) During the course of the coagulation
process, a temperature gradient is generated between center and outside
of the coagulation vessel, leading to convection flows, which counteracts
further gravity-induced coagulation, making pair formation successful in
only part of the expected collisions.
The alternative sub a) must be dismissed since it can be calculated that
particle aggregates must have dimensions of the order of 30 m
m in order to be removed to a significant extent from the space between
the measuring spot and the top of the vessel (distance 4 cm). The second
alternative is in line with what will be reported in chapter 5, and will
therefore be adopted here as explanation of the decrease of transmitted
light intensity at the backside of the peak.
A preliminary calculation of the force necessary to separate two particles
with diamter 1 m m and 3 m
m respectively, by gravity (without taking into account shear forces from
convection flows) has been reported by the method of Dukhin (appendix A).
Let us now analyze the forces involved during the sedimentation
of a doublet of different particle sizes according to Dukhin, appendix A.
Equations (A.8), (A.3) and (A.4) of appendix A, make it possible to calculate
the forces acting on the particles of an aggregate by the surrounding liquid
under steady state sedimentation conditions. When we apply this analysis
to our system, the detachment force for the larger particle is found to
be in the order of 10-14 N. In the calculations performed a1
was equal to 3.230 m m and a2
was equal to 1.288 m m and a
=2.51 (see appendix A).
The importance of this observation is, that two particles on the point of making contact can be separated by the hydrodynamical forces exerted on them by flows in the surrounding liquid. We will return to this point in chapter 5.
4.5 Comparison of the experimental coagulation rates with the theoretical value of von Smoluchowski.
The von Smoluchowski theory [17] considering only Brownian motion predicts a value for the rate constant of k11 = 10.77 * 10-12 p-1 cm3 sec-1 for water at 20° C. Rate constants of our experimental data were calculated with an equation used by Lichtenbelt et al. [18,19]:
k11 = ((1/E0)(dE/dt)0)/[((C2/2C1)-1)N1]
where E is extinction (related to the transmission by E=-logT), t is time, and C1 and C2 are the extinction cross sections of a singlet and of a doublet, respectively. The subscript zero refers to the limiting case of t ® 0. The initial particle concentration N1 was determined from the dry weight of the latex. The value was 2.387*107 p cm-3, where p is the number of particles. The resulting values of k11 for the 1g (density matched), 1g (pronounced density difference) and the µg experiments are given in Table 4.2.
Table 4.2: The coagulation rate constant, expressed as k11 (p-1 cm-3 sec-1), and as a percentage of the von Smoluchowski value for L-93.
|
Experiments |
k11 * 1012 |
% |
Lichtenbelt [19] |
|
1g (density difference) |
0.754 |
7 |
40-60% |
|
1g (density matched) |
2.046 |
19 |
|
|
µg |
8.616 |
80 |
|
|
von Smoluchowski |
10.77 |
100 |
|
The values for the rate constants at
1g are low compared with results found by Lichtenbelt et al. [19]. A possible
explanation for the difference with our results is that the diameter of
our particles is approximately six times larger than the particles of Lichtenbelt
used, but there is no dependence on the diameter expected for the rate constants.
However, retardation of London-van der Waals attraction is more important
for larger particles. Of course there is a difference in the velocity of
sedimentation, which is in the case of Lichtenbelt's experiments a factor
36 slower. This leads to a longer contact time of the particles. Also the
volume fractions in the experiments of Lichtenbelt were approximately two
times larger. A possible explanation of the difference is that the factors
retarding coagulation at 1g (see chapter 5) are operative to a greater extent
for large than for small particles.
Fact is that at µg -conditions the theoretical
value of the rate constant according to von Smoluchowski is best approached.
Apparently, µg -conditions best reflect the assumptions made by von Smoluchowski
in which hydrodynamic interactions and interparticle forces are ignored,
and particles will solely coagulate under influence of Brownian motion.
4.6 Video analysis of the perikinetic coagulation process
Experimental
Optical
evidence on what happens during the perikinetic coagulation process has
been obtained by an experimental set-up in which the coagulation process
could be visualized by means of a ccd camera and a microscope as illustrated
in Figure 4.10. The basic apparatus of this set-up, is a Rank-Brothers MK
11 electrophoresis cell as normally used to determine z -potentials. A microscope
with a ccd camera (HCS MXR) and a monitor (effective enlargement of this
combination: 1000 times) with a video recorder were attached to the Rank-Brothers
MK 11. With this setup it is possible to visually observe two particles
interacting during the coagulation process.
A cell (dimensions: 70 mm x 8 mm x 0.7 mm), containing the dispersion, was placed in a thermostated water reservoir; the experiments were performed at a reservoir temperature of 20 ± 0.1 ° C. Experiments were performed with a dispersion of silica and two dispersions of polystyrene (L-93), one with the densities nearly matched by means of D2O (D r =1 kg/m3), and one with a distinct density difference (D r =-31 kg/m3). Two particles were analyzed by registering their `projected interaction distance' (i.e. the projection of the distance between two particle centers on a plain perpendicular to the direction of observation) and the `projected interaction angle' (i.e. projection of the angle between the line connecting two particle centers and the direction of gravity ,on a plain perpendicular to the direction of observation). The particle concentration was the same as in the coagulation experiments performed in chapter 3 and this chapter. The experiments were recorded on video tape and analyzed afterwards.
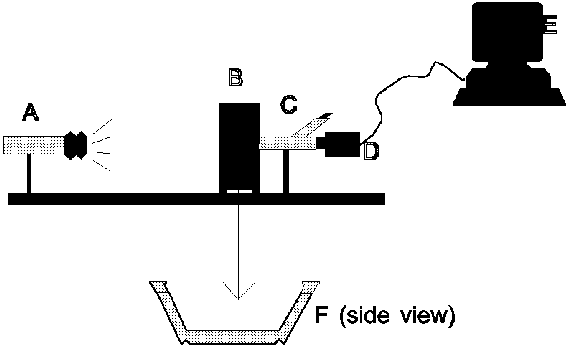
Figure 4.10 Experimental set-up; A: light source, B: thermostated water reservoir, containing a capillary (F), with two bends as used in a traditional Rank Brothers electrophoresis unit, with the dispersion, C: microscope, D: ccd camera, E: monitor, F: capillary.
Results & Discussion
Figures
4.11 and 4.12 show the results of the video analysis. When looking at figure
4.11, the polystryrene dispersion with a density difference of -31 kg/m3,
the following behaviour was observed:
(i) particles approach each other, due
to sedimentation and Brownian motion,
(ii) particles interact, start to oscillate at
low frequencies, and their interaction angle changes,
(iii) particles lose contact.
For the polystyrene dispersion in which the density was matched, a different behaviour was observed, the interaction times are longer: the particles stay in each others proximity. Figure 4.12 plots the projected interaction distance (as defined above) as a function of time for both dispersions. From each dispersion the behaviour of 10 doublets was analyzed; only those pairs of particles were chosen who finally formed a doublet which remained at least temporarily combined (`transient' or `permanent' doublet). From this plot it can be seen that the interaction times in the case of the density matched dispersion are longer.
Observations possibly related with the findings reported here have been mentioned by Hofman [7].
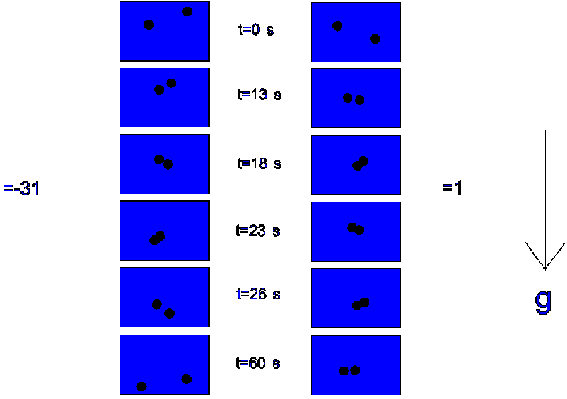
Figure 4.11: Interaction times of two particles, in the case of a density difference of -31 kg/m3 and a density difference of 1 kg/m3.
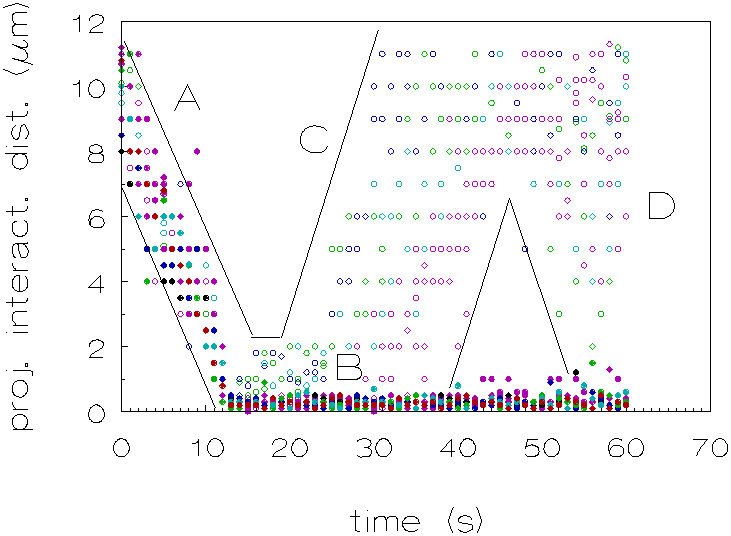
Figure 4.12: Projected interaction distance as a function of time, for D r =-31 kg/m3 (¡ ) and D r =1 kg/m3 (l ). A: particles approach each other, B: particles interact during a certain period, C: some particles move away from each other and D: some particles approach new particles.
Hofman's experiments showed a higher coagulation rate when the density difference between disperse and continuous phase was small. A possible explanation Hofman gives for his results is that due to slower sedimentation, the particles will be longer in contact during a collision, and the probability of cluster formation higher (see also p.54).
Our video analysis of the perikinetic
coagulation process indeed shows longer interaction times for the density
matched dispersion.
The changes in the interaction angle can be explained
as follows: as the particles approach one another, the viscous resistance
to motion increases, particularly along the line of centers, hence the magnitude
of the Brownian forces must increase to maintain the prescribed kinetic
energy. For two spheres in contact (or nearly in contact) this corresponds
to a rotational diffusion of the doublet, since translational diffusion
along the axis is slightly faster than the transverse process [20].
The changes in the projected interaction distance,
when the particles interact (period C, in Figure 4.12) during a certain
period of time, are in the order of 1 to 5*10-7 m. The corresponding
frequencies for these oscillations are in the order of 0.4 s-1.
It should be noted that the above mentioned values are rough estimates,
only 20 pairs of particles were analyzed and projected interaction distances
are difficult to determine because distances are determined from a monitor
screen in 2D and the dimensions of the particles on the screen are very
small. This makes it difficult to determine the actual projected interaction
distances precisely. During the experiments also free convection currents
were observed even at small temperature changes of ± 0.1 ° C of the surrounding
thermostated water. These currents were observed through sudden movements
of the particles in horizontal or upward directions for particles who were
sedimenting.
The influence of such free convection on the coagulation
behaviour will be discussed in chapter 5.
4.7 Conclusions
1) In the absence of a density difference between disperse and continuous phases, perikinetic coagulation is faster than in the presence of such a density difference.
2) The most pronounced effect of high-gravity on coagulation rate is found for dispersions with a small density difference, on going from 1g to 2g. In this regime a significant decrease in coagulation rates is observed. For higher g-levels, no change or an increase in coagulation rate is observed.
3) There are differences between the densities of separate PS-particles. So it is impossible, under terrestrial conditions, to match the densities of the continuous phase and dispersed phase, exactly.
4) For the latex mixture at pronounced density differences, gravity induced coagulation was observed, however the formed doublets did not have a lasting contact, which indicates an influence of convection flows increasing with increasing temperature gradients in the system during the course of an experiment. After calculation of the bulk forces acting on the particles, it turned out that the detachment force for the larger particle of the formed doublet is in the order of 10-14 N.
5) Comparison of the experimental rate constants with the theoretical value of von Smoluchowski, showed that the rate constant calculated at µg -conditions approaches the value of von Smoluchowski. Apparently, µg -conditions best reflect the assumptions made by von Smoluchowski in which hydrodynamic interactions and interparticle forces are ignored, and particles will solely coagulate under influence of Brownian motion.
6) From the video analysis it can be concluded that the interaction times for a density matched dispersion are longer and that doublets of particles are easily disrupted when sedimentation is operative. Free convection currents may influence the formation and disruption of pairs of particles.
References
(1) Krutzer, L.L.M., The influence of Flow Type,
Particle Type and Gravity on Orthokinetic Coagulation, 1993,
Ph. D. Thesis, Eindhoven.
(2)
van Diemen, A.J.G., Stein, H.N., J. Colloid Interface Sci.,
1983, 96, 150.
(3)
Logtenberg, E.H.P., The Relation between the Solid State Properties
and the Colloidal Chemical Behaviour of Zinc Oxide, 1983,
Ph. D. Thesis, Eindhoven University of Technology.
(4)
Brakalov, L.B., Chem. Eng. Sci., 1987, 42, 2373.
(5)
Ven, van de T.G.M., Mason, S.G., Colloid Polym. Sci., 1977,
255, 794.
(6)
Zeichner, G.R., Schowalter, W.R., Assoc. Ind. Chem. Eng. J.,
1977, 23, 243.
(7)
Hofman, J.A.M.H., Flow of Dilute Emulsions through Poreus Media,
1990, Ph. D. Thesis, Eindhoven University of Technology.
(8)
Tuin, G., Peters, A.C.I.A, Diemen, van A.J.G., Stein, H.N., J.
Colloid Interface Sci., 1993, 158 (2), 508.
(9)
Schott Group, Viscosity Measuring Unit AVS-310, Schott Geräte
GMBH, Hofheim a. Ts., 1987, Germany.
(10)
Muller, H., Kolloidchem. Beih., 1928, 26, 257.
(11)
Matthews, B.A., Rhodes, C.T., J. Colloid Interface Sci.,
1970, 32, 332.
(12)
Ho, N.F.H., Higuchi, W.I., J. Pharm. Sci., 1968, 57,
436.
(13)
Verdegan, B.M., Anderson, M.A., J. Colloid Interface Sci.,
1993, 158, 372.
(14)
Melik, D.H. Fogler, H.S., J. Colloid Interface Sci., 1984,
101, 84.
(15)
Wang, Y.G., Wen, C.S., J. Fluid Mech., 1990, 214,
599.
(16)
Wen, S., Zhang, L., Lin, H., J. Colloid Interface Sci., 1991,
142, 257
(17)
Smoluchowski, von M., Physik. Z. ,1916, 17,
557; 1916, 17, 585; Z. Phys. Chem., 1917,
92, 129.
(18)
Lichtenbelt, J.W.Th., Ras, H.J.M.C., Wiersema, P.H., J. Colloid
Interface Sci., 1974, 46 (3), 522.
(19)
Lichtenbelt, J.W.Th., Pathmamanoharan, C., Wiersema, P.H., J.
Colloid Interface Sci., 1974, 49 (2), 281.
(20)
Russel, W.B., Saville, D.A., Schowalter, W.R., Colloidal Dispersions,
Cambridge University Press, New York, 1989, chapter 3.