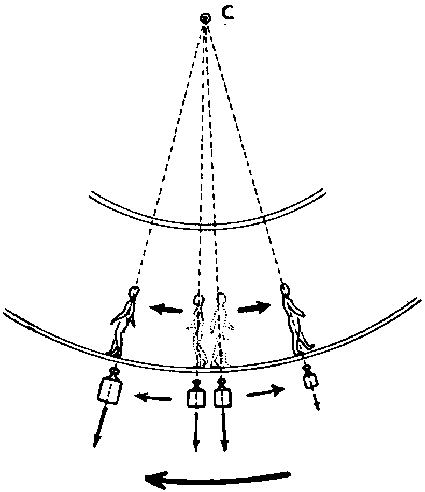
Fig. 8 toont de baan van een .,vrijvallend" voorwerp binnen de satelliet. Het voorwerp komt, gerekend ten opzichte van de draairichting der satelliet, achter het verwachte punt op de vloer.
HOOFDSTUK 4
DYNAMISCHE VERHOUDINGEN
De dynamische verhoudingen waaronder de ruimtevaarder zich zal bevinden bieden geheel nieuwe en nog moeilijk voorspelbare physiologische consequenties.
Zowel bij verblijf in een satelliet als tijdens een eventuele vaart in de ruimte zal de reiziger in een semi-permanent toestand van gewichtsloosheid verkeren. Immers de voortstuwingsversnellingen die zowel in het eerste als in het tweede geval nodig zijn om het vaartuig zijn koers te geven zullen slechts gedurende korte ogenblikken werkzaam zijn. De overige tijd is de reiziger gewichtsloos in zijn gewichtsloze omgeving. Men is geneigd de situatie te beschouwen en te beschrijven als een van zweven. Hier bestaat, naar ik meen, geen bezwaar tegen indien men het zweven van een lichaam in een vloeistof of gas bedoelt wanneer lichaam en vloeistof eenzelfde soortelijk gewicht hebben en het een homogeen lichaam betreft, Dat is n.l. in de ruimtevluchtsituatie voor alle lichamen het geval doordat het S.G. dan steeds gelijk, n.l. 0, is.* (*:Het S.G. is hierbij gedefinieerd als: (gravitatie + inertieversnelling op 1 cc. stof)/gravitatie + inertieversnelling op 1 cc. water))
Het zou echter misleidend zijn indien men in gedachten de situatie zou vergelijken met die van het zweefvliegen; immers hier is het S.G. van vliegtuig en omgeving geenszins gelijk doch weet men gedurende enige tijd dit verschil te compenseren door kunstig gebruik te maken van uitwendige krachten. Ik geloof dat het daarom physisch zowel als physiologisch juister is het gewichtsloos in de ruimte zijn te vergelijken met onderwater zwemmen. Men kan mij dan tegenwerpen dat er daarbij in het lichaam zelf nog verschillen in S.G. blijven bestaan, hetgeen bij het ruimte-zweven niet het geval is. Inderdaad is dit ook zo en het zal noodzakelijk zijn hieraan speciaal aandacht te schenken.
Met name wordt aan de belangrijke otolithaire functie in de toestand der gewichtsloosheid het zwijgen opgelegd. (62a, 68)
Wanneer men nochtans de gewichtsloze toestand mag vergelijken met het onderwater zwemmen en onderwater zweven dan zal deze situatie physiologisch weinig bezwaar kunnen opleveren. Er is dan nog één maar bij dit alles en dat is het verschil in physische eigenschappen (viscositeit - of, algemener, wrijving en soortelijke dichtheid) tussen lucht en water.
Stellig zal dit de locomotorische verhoudingen tot geheel andere maken; de statische verhoudingen van het lichaam als geheel laat het echter ongewijzigd ten opzichte van de onderwatersituatie. Met deze statische verhoudingen bedoel ik de perceptie van de lichaamsstand en van de ledematen en haar onderdelen onderling. Waaruit zal de ruimtereiziger zijn informatie moeten putten omtrent de stand van zijn eigen lichaam? Het been zweeft gewichtsloos aan de romp, het onderbeen aan het bovenbeen, de voet aan het onderbeen enz. Trek- en drukverschijnselen verzaken hun plicht om het lichaamsbeeld te vormen en de mens is aangewezen op zijn visuele indrukken om zijn lichaamsstand te kennen. Dat zou voorwaar een bedenkelijke situatie zijn die een sluimerend narcisme tot ongekende proporties zou kunnen doen aanzwellen.
Ik meen dat dit alles mee zal vallen en wel om de volgende reden: Weliswaar zal het ene lichaamsdeel trek noch druk op het andere uitoefenen maar de stand der gewrichten kan ook op andere wijze gekend worden. Men zou - om zich een beeld van de lichaamsperceptie bij gewichtsloosheid te vormen - een analogie kunnen trekken met de kennis over de stand der oogbol zonder visuele indruk. De structuren binnen de oogkas verschillen niet in S.G.; uitwendige druk of trek biedt geen aanknopingspunt voor standsindrukken en toch is het zeer wel mogelijk ook in het duister of achter gesloten oogleden te weten hoe de oogbol gericht is.
Keren wij nu terug tot de locomotorische verhoudingen in het ruimteschip. Terwijl voor het ruimtezweven, zoals boven uiteen- gezet, de analogie met de immersie-toestand in water tot op zekere hoogte verantwoord lijkt, gaat voor het "ruimtezwemmen" deze vergelijking met het onderwaterzwemmen mank. De wrijving en soortelijke dichtheid zijn zo geheel verschillend bij lucht en bij water dat eenzelfde spieractie in het ene geval een locomotorisch vele malen grotere reactie uitlokt dan in -het andere.
Om niet in voortdurend mechanisch conflict met zijn omgeving te geraken zal de ruimtevaarder dus buitengewoon behoedzaam in zijn handel en wandel - in dit geval in de meest letterlijke zin bedoeld -moeten zijn. Geeft de ruimtevaarder met stap of sprong zijn lichaam een versnelling dan zal de snelheid voortduren totdat hij - in botsing komend met wand of plafond een nieuwe versnelling in tegengestelde richting krijgt. Daarom schijnt het mij aanbevelenswaardig toe de binnenwanden van het ruimteschip zowel als de tafels en stoelen en andere objecten glad te houden met ronde hoeken en zo mogelijk bedekt met een zacht verend materiaal b.v. schuimrubber.
De ruimtevaarder zal naar alle waarschijnlijkheid moeite hebben om zich de gewenste behoedzaamheid eigen te maken. Dit impliceert naar mijn mening niet dat hij zijn spieren practisch op non-actief moet stellen en hiermee een inactiviteitsatrophie willens en wetens moet riskeren. Een fijnzinnige beheersing van de antagonistisch werkende spieren behoeft immers niet een vrijwel lamleggen der motoriek in te houden. Hoe dit alles zij, de physiologische adaptatie aan de gewichtsloosheid blijft een probleem dat slechts in de ruimtevaart zelve tot oplossing gebracht kan worden. De kortdurende experimenten met parabolische vluchten kunnen nauwelijks geacht worden in dit verband relevant te zijn. Zij hebben aangetoond dat de coördinatie van fijne bewegingen b.v. schrijven ernstig bemoeilijkt is (von Beckh, 5a en Haber, 47a)
Vooruitlopend op de verdere bespreking in het 6e hoofdstuk geloof ik wel te kunnen zeggen dat men een gerede twijfel mag koesteren of de adaptatie aan een zo ongewone situatie als door gewichtsloosheid gegeven, vloeiend en vlot tot stand zal komen; vooralsnog lijkt dit op zín minst dubieus en het ligt dan ook voor de hand dat men gezocht heeft naar een mogelijkheid de ruimtevaarder opnieuw gewicht te geven.
In het voorgaande werd de mens in de ruimtevaart gewichtsloos gedacht in zijn gewichtsloze omgeving. Er bestaat echter een mogelijkheid om de moeilijkheden van deze situatie te doorbreken.
Een nieuw gewicht, een gewicht anders dan door de gravitatie gegeven, kan namelijk verkregen worden door het invoeren van een inertiekracht. Men bereikt dit door het ruimteschip te laten roteren om zijn eigen as. De versnelling der inertiekracht die men daarmee opwekt is recht evenredig met het kwadraat van de hoeksnelheid en met de straal: b=W2R.
In het vorige hoofdstuk werden reeds enige constructiegedachten over de bemande aardsatelliet vermeld. Zoals gezegd stelt Von Braun zich deze voor als een groot wiel met een straal van 40 m. draaiend om zijn eigen as met een hoeksnelheid van 2/7 radiaal per seconde. De as zal evenwijdig moeten lopen met de as waaromheen de satelliet zijn baan om de aarde beschrijft.
Dit afrollen langs de eigen baan is technisch noodzakelijk omdat daardoor een stabiele loop verzekerd is. De satelliet verkrijgt aldus een gyroscopische stabiliteit terwijl hij te zelfder tijd de inzittenden een traagheidsversnelling verleent, die voor hen het verlies der gravitatie compenseert. Door de afplatting der aarde zal de satelliet toch enige precessie ondervinden die hem uit zijn gekozen baan poogt te drijven. Het zal noodzakelijk zijn met behulp van raketmotoren deze precessiekracht te compenseren.
De centrifugale versnelling die de satellietinzittenden in het door Von Braun gedachte schema zullen ondervinden bedraagt W 2R = (2/7)2 ◊ 4000 cm/sec2 = 327 cm/sec2.
Om in de gebruikelijke terminologie te blijven is dit dus ongeveer 1/3 G. Nu kan men er uitvoerig over discussiëren of een drievoudige vermindering van de normale - door gravitatie veroorzaakte - richtkracht tot physiologische aanpassingsmoeilijkheden zal leiden, maar het schijnt toch wel boven twijfel verheven dat deze situatie aanmerkelijk gunstiger is dan de totale afwezigheid van gravitatie en inertiekracht. In principe is door het vicariërend invoeren van de centrifugale versnelling de mogelijkheid gegeven om iedere willekeurige G.-waarde te bereiken. Men zal dan slechts hetzij de W hetzij de R hetzij W en R van de satelliet anders moeten concipiëren. Dit lijkt alles heel fraai ware het niet dat er een adder onder het gras schuil ging; een adder, die - om deze beeldspraak voort te zetten -over een bijzonder verraderlijk venijn beschikt. Laat ik dit nader mogen toelichten.
In de eerste plaats noem ik dan de abnormale baan die een zgn. -vrijvallend voorwerp in de satelliet beschrijft.
Stellen wij de kamerhoogte op 4 meter dan zal zoín voorwerp tijdens de -vrije val- zijn tangentiele snelheid continuerend zich rechtlijnig verplaatsen van A naar B en in B op de vloer terecht komt (fig. 8). Bij het begin der val hing het voorwerp loodrecht boven C. Punt C verplaatst zich nu in de 40 valperiode over een booglengte CD = 40/36 ◊ de afstand AB. Een eenvoudige berekening leert nu dat punt B en punt D niet samenvallen en dat het voorwerp dus - beschouwd door de satellist - niet loodrecht op de grond valt.
AB = Ö(402
- 362)= 17.43
CD =10/9 AB = 19.37
Verder is cosa
= 36/40
waaruit bij benadering volgt a
= 26į = 0.45 rad. (in werkelijkheid iets meer)
en BC = a
r = 0.45 ◊ 40 = 18 (in werkelijkheid 18.04)
dus is BD = CD = 19.37 - 18.04 = 1.33
Uit de bovenstaande berekening blijkt dat een voorwerp, vrij vallend van het plafond der satellietkamer, op 1.33 m. achter het verwachte punt op de bodem komt. Het 'valt' dus niet alleen veel langzamer dan normaal maar het 'valt' ook anders n.l. niet loodrecht van plafond naar bodem. Ik heb dit ongewoon patroon willen mentioneren niet omdat ik meen dat het een onoverkomelijk struikelblok voor de ruimtevaart zal blijken te zijn maar omdat de ruimtevaarder er op attent zal dienen te zijn en er zich aan zal moeten aanpassen. Als zodanig is het wel degelijk een ruimtevaartgeneeskundig probleem.
De vervanging van de gravitatie door de centrifugale richt- kracht brengt -ik duidde dat boven reeds aan - nog een onverwachte en bijzonder verraderlijke consequentie met zich. Het betreft de reacties die er door in het argeloze evenwichtsorgaan kunnen worden uitgelokt. Aangezien het daarbij - voor wat betreft de halfcirkelvormige kanalen - om een specifiek zintuigpsysiologisch probleem gaat wil ik dit in het volgende hoofdstuk bespreken.
Als introductie daartoe wil ik dit hoofstuk besluiten met een meer algemeen, zij het minder belangrijk aspect.
De radiaire versnelling, die de plaats moet innemen van de op aarde ondervonden gravitatie brengt met zich mede, dat vloeren, tafels en in principe alle "aequi-acceleratie vlakken" aan de kromtestraal van de satelliet zullen moeten beantwoorden indien men wil voorkomen, dat vloeistoffen en rollende voor- werpen zich naar de twee wanden der satellietkamer bewegen.

Fig. 8 toont de baan van een .,vrijvallend" voorwerp binnen de satelliet. Het
voorwerp komt, gerekend ten opzichte van de draairichting der satelliet, achter
het verwachte punt op de vloer.
Voor de benoeming der kamerwanden, stellen wij ons de satelliet - als steeds - voor in de zin van Von Braunís conceptie. Gemakshalve kunnen we dan spreken van een:
1. zonzijde;
2. schaduwzijde;
3. vloer of buitenzijde;
4. plafond of binnenzijde;
5. zijwanden.
Deze zijwanden zouden wij dan weer kunnen onderscheiden in voor- en achterwand met betrekking tot de draairichting der satelliet.
Een dergelijke - mechanisch verantwoorde - uitgeholde kamervorm biedt echter talloze practische bezwaren als daar zijn: het werken op een holle tafel, het plaatsen van voorwerpen op zoín tafel. Stoelen op een concave vloer zijn al evenmin ideaal en - zuiver physiologisch - vraag ik me af, of het aangenaam is, te moeten lopen over een dergelijke vloer. Ik vrees, dat de orthopaed reeds klaar staat met het ziektebeeld der satelliet- voeten, als ruimte-variant op de "aards" banale plat- en knikvoet.
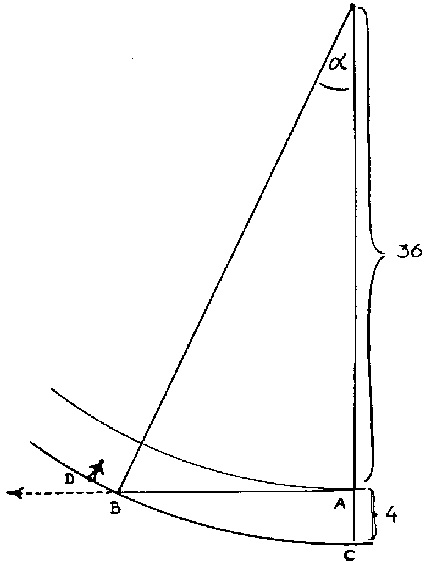
Fig. 9. Meelopend met de draairichting der satelliet vermeerdert het gewicht;
tegenlopend neemt het af.
De Radiaire versnelling als vervanger van de gravitatie impliceert tenslotte, dat iedere beweging met de draairichting der satelliet mee tot gewichtsvermeerdering leidt en omgekeerd iedere beweging tegen de draairichting van de satelliet in tot gewichtvermindering. Zo zien wij dan, dat de satellist - zich van geen kwaadbewust - continu van gewicht verandert, wanneer hij door zijn compartiment kuiert om enige lichaamsbeweging te nemen. Versnelt hij zijn pas, dan stijgt zijn gewicht verder, resp. neemt verder af en wel met het kwadraat van zijn absolute tangentiële snelheid (satellietsnelheid + bewegingssnelheid, fig. 9). Immers is de centrifugale versnelling b = V2/r
De tangentiële snelheid van de satelliet is te berekenen uit de formule V = W r
In Von Braunís ontwerp zijn de waarden van W en r resp. 2/7 radiaal per seconde en 40 m waaruit volgt dat V ruim 41 km/uur bedraagt.
Wil de satellist nu b.v. zijn gewicht verdubbelen resp. halveren dan zal hij zich moeten voortbewegen met een snelheid van (41Ö 2 - 41)= 17 km/uur met de draairichting van de satelliet mee resp. (41 Ė 41/Ö 2) = 12 km/uur tegen de draairichting van de satelliet in.
De satellist, zo meen ik te mogen veronderstellen, zal deze gewichtswijzigingen ervaren als liftsensatie en wel gewichtsvermeerdering als stijgen en gewichtsvermindering als dalen. Deze veronderstelling is gegrond op de liftsensaties die - speciaal ook in de luchtvaart - bestudeerd zijn bij verhoging en verlaging der g-waarden. Weliswaar is de "rust" waarde dan steeds 1 g en niet zoals in de satelliet 1/3 g maar dit zal geen principieel verschil kunnen maken.
De gevoelige receptoren voor de lineaire versnellingen, waar het hier om gaat, zijn te vinden in het otolithen systeem.
In werkelijkheid is de situatie nog gecompliceerder. Er ontstaat nl. bovendien een contradictie in de zintuigelijke indrukken onderling. Bij een vlakke vloer staat de centrifugale versnelling in de uiteinden der kamer niet loodrecht op de vloer. Mee- of tegenlopend met de draairichting der satelliet zal de satellist dit ondervinden als een progressieve standsverandering van het lichaam van achteroverhellend tot vooroverhellend, fig. 10.
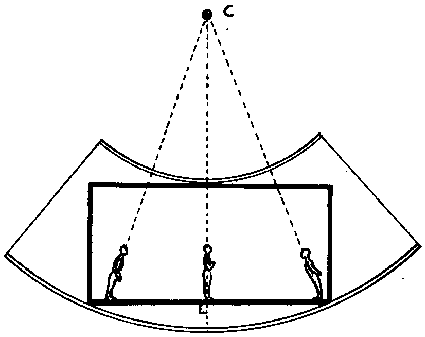
Fig. 10. In een satellietkamer met vlakke vloeren zal de lichaamsstand t.o.v.
de kamervertikaal variëren met de positie in de kamer.
Is de vloer niet vlak maar gebogen volgens de omtrek der satelliet, dan zal eveneens een conflicterende informatie uit de verschillende zintuigelijke receptoren resulteren.
Inmiddels zijn wij beland op het terrein der
zintuigphysiologie waarover in het volgende hoofdstuk meer.